1362 字
7 分钟
🌳二叉树从基础概念到应用实践

一、树型结构基础
1.1 树的基本概念
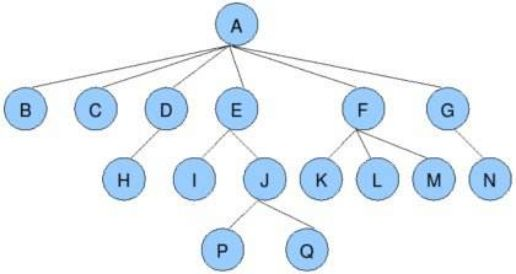
树是一种非线性的数据结构,由n(n>0)个有限节点组成一个具有层次关系的集合。它看起来像一棵倒挂的树,根朝上而叶朝下。
关键特点:
- 有且仅有一个根节点,没有前驱节点
- 除根节点外,其余节点被分成M(M>0)个互不相交的子树
- 树是递归定义的
重要术语:
- 结点的度:一个结点含有子树的个数
- 树的度:树中所有结点度的最大值
- 叶子结点:度为0的结点
- 双亲结点/父结点:含有子结点的结点
- 孩子结点/子结点:一个结点含有的子树的根结点
- 根结点:没有双亲结点的结点
- 结点的层次:从根开始定义,根为第1层
- 树的高度/深度:树中结点的最大层次
1.2 树的表示方法
最常用的表示方法是孩子兄弟表示法:
class Node { int value; // 树中存储的数据 Node firstChild; // 第一个孩子引用 Node nextBrother; // 下一个兄弟引用}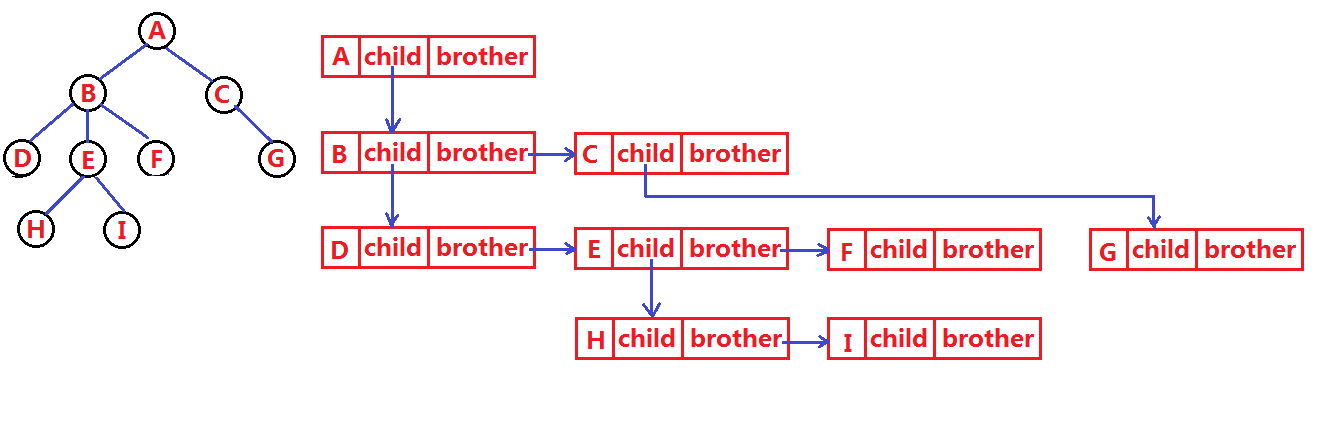
二、二叉树详解
2.1 二叉树概念
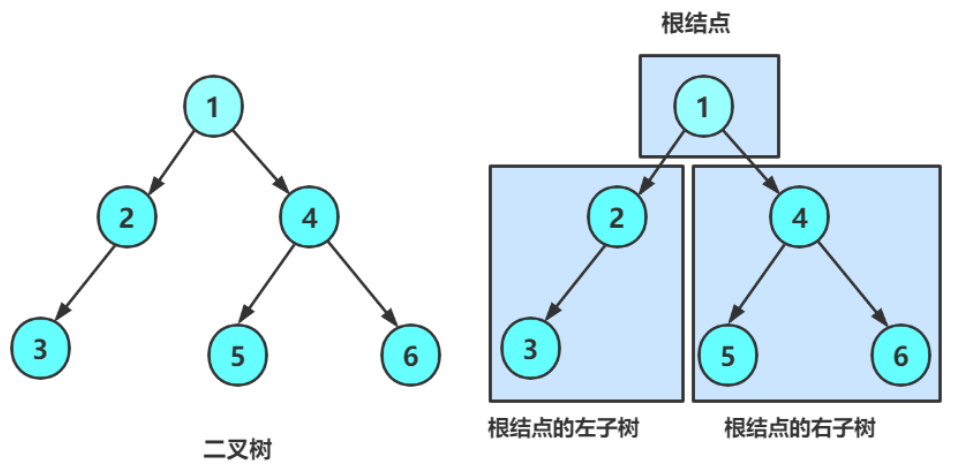
二叉树是结点的一个有限集合,该集合:
- 或者为空
- 或者由一个根节点加上两棵分别称为左子树和右子树的二叉树组成
特点:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,是有序树
2.2 特殊二叉树
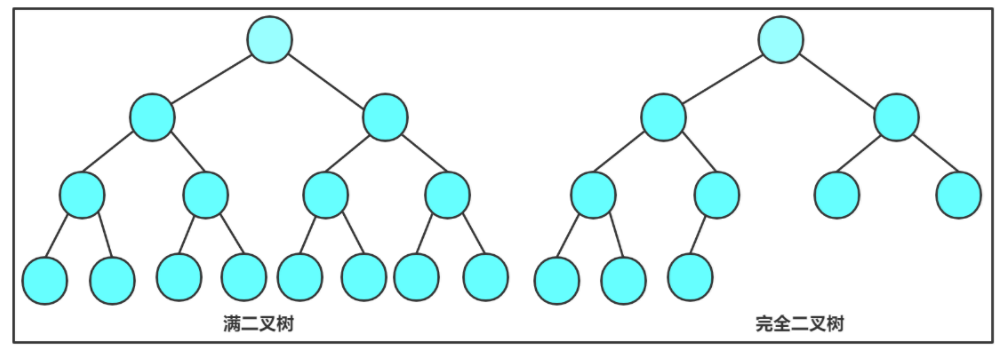
- 满二叉树:每层的结点数都达到最大值。层数为K,结点总数是2^K-1
- 完全二叉树:深度为K,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应
2.3 二叉树的性质
- 非空二叉树的第i层最多有2^(i-1)个结点
- 深度为K的二叉树最大结点数是2^K-1
- 对于任何二叉树,n0(叶子结点) = n2(度为2的结点) + 1
- 具有n个结点的完全二叉树深度为⌈log₂(n+1)⌉
- 完全二叉树的父子结点关系:
- 父结点序号:(i-1)/2
- 左孩子序号:2i+1
- 右孩子序号:2i+2
2.4 二叉树的存储
链式存储
// 孩子表示法class Node { int val; // 数据域 Node left; // 左孩子引用,常常代表左孩⼦为根的整棵左⼦树 Node right; // 右孩子引用,常常代表右孩⼦为根的整棵右⼦树}
// 孩子双亲表示法class Node { int val; Node left; // 左孩子引用,常常代表左孩⼦为根的整棵左⼦树 Node right; // 右孩子引用,常常代表右孩⼦为根的整棵右⼦树 Node parent; // 当前节点的根节点}三、二叉树遍历
遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做⼀次且仅做⼀次访问。访问结点所做的操作依赖于具体的应⽤问题(比如:打印节点内容、节点内容加1)。遍历是⼆叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
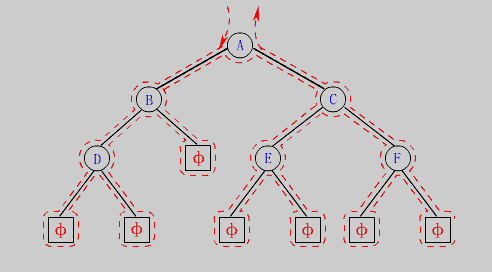
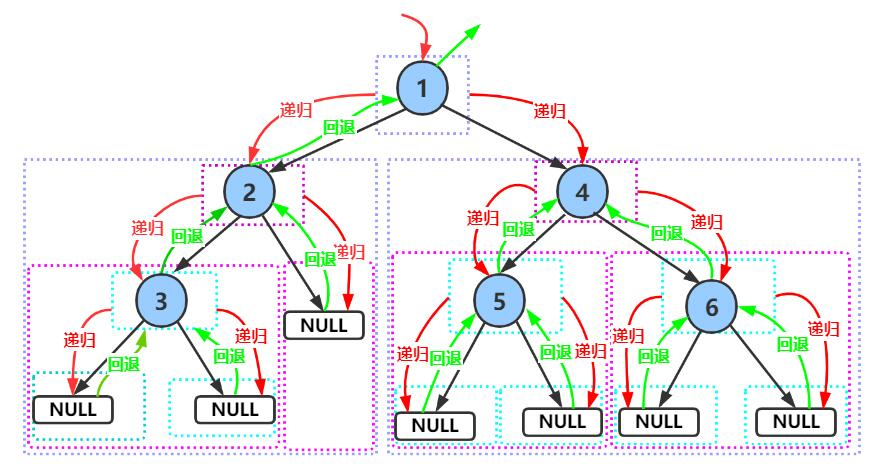
3.1 递归遍历
- (NLR)前序遍历:根节点 -> 左子树 -> 右子树
- (LNR)中序遍历:左子树 -> 根节点 -> 右子树
- (LRN)后序遍历:左子树 -> 右子树 -> 根节点
// 前序遍历void preOrder(Node root) { if (root == null) return; System.out.print(root.val + " "); preOrder(root.left); preOrder(root.right);}
// 中序遍历void inOrder(Node root) { if (root == null) return; inOrder(root.left); System.out.print(root.val + " "); inOrder(root.right);}
// 后序遍历void postOrder(Node root) { if (root == null) return; postOrder(root.left); postOrder(root.right); System.out.print(root.val + " ");}3.2 层序遍历
从根节点出发,按层次从上到下、从左到右访问结点。
void levelOrder(Node root) { if (root == null) return; Queue<Node> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { Node cur = queue.poll(); System.out.print(cur.val + " "); if (cur.left != null) queue.offer(cur.left); if (cur.right != null) queue.offer(cur.right); }}四、二叉树基本操作
代码示例:
// 获取节点个数int size(Node root) { if (root == null) return 0; return 1 + size(root.left) + size(root.right);}
// 获取叶子节点个数int getLeafNodeCount(Node root) { if (root == null) return 0; if (root.left == null && root.right == null) return 1; return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}
// 获取第k层节点个数int getKLevelNodeCount(Node root, int k) { if (root == null || k <= 0) return 0; if (k == 1) return 1; return getKLevelNodeCount(root.left, k-1) + getKLevelNodeCount(root.right, k-1);}
// 获取二叉树高度int getHeight(Node root) { if (root == null) return 0; return 1 + Math.max(getHeight(root.left), getHeight(root.right));}
// 查找值为val的节点Node find(Node root, int val) { if (root == null) return null; if (root.val == val) return root; Node left = find(root.left, val); if (left != null) return left; return find(root.right, val);}结语
二叉树是数据结构中的核心内容,掌握好二叉树对于理解更复杂的数据结构和算法至关重要。建议读者在学习理论的同时,多动手实现代码,解决实际问题,才能真正掌握二叉树的精髓。
🌳二叉树从基础概念到应用实践
https://mizuki.mysql.com/posts/datastructure/e/content/ 



